MATHS

Question 1:

(a) The cost of 1 kg of tomatoes is $x and the cost of 1 kg of onions is $y.
Ian pays a total of $10.70 for 10 kg of tomatoes and 4 kg of onions.
Jao pays a total of $10.10 for 8 kg of tomatoes and 6 kg of onions.
Write down simultaneous equations and solve them to find \( x \) and \( y \).
Answer: \( x = \) .................................................
\( y = \) ................................................. [6]

(b) Solve \[ 2x^2 - 5x - 8 = 0 \]
Give your answers correct to 2 decimal places. Show all your working.
Answer: \( x = \) ................................................. or \( x = \) ................................................. [4]

Question 2:

(a) Rice costs $x per kilogram.
Potatoes cost $(x + 1) per kilogram.
The total cost of 12 kg of rice and 7 kg of potatoes is $31.70.
Find the cost of 1 kg of rice.
Answer: $ ................................................. [3]

(b) The cost of a small bottle of juice is $y.
The cost of a large bottle of juice is $(y + 1).
When Catriona spends $36 on small bottles only, she receives 25 more bottles than when she
spends $36 on large bottles only.
(i) Show that \( 25y^2 + 25y - 36 = 0 \).
Answer: ................................................. [3]

(ii) Factorise \( 25y^2 + 25y - 36 \).
Answer: ................................................. [2]

(iii) Solve the equation \( 25y^2 + 25y - 36 = 0 \).
Answer: \( y = \) ......................................... or \( y = \) ......................................... [1]

(iv) Find the total cost of 1 small bottle of juice and 1 large bottle of juice.
Answer: $ ................................................. [1]

Question 3:

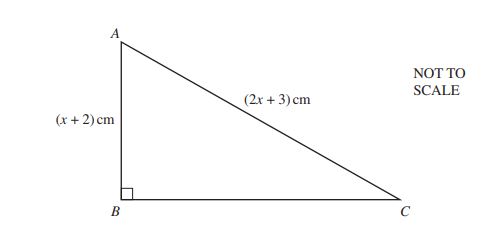
(a) In triangle ABC, \( AB = (x + 2) \) cm and \( AC = (2x + 3) \) cm.
\(\sin ACB = \frac{9}{16} \).
Find the length of \( BC \).
Answer: \( BC = \) ......................................... cm [6]

(b) A bag contains 7 white beads and 5 red beads.
(i) The mass of a red bead is 2.5 grams more than the mass of a white bead.
The total mass of all the 12 beads is 114.5 grams.
Find the mass of a white bead and the mass of a red bead.
Answer: White = ............................................ g
Red = ............................................ g [5]

(ii) Two beads are taken out of the bag at random, without replacement.
(a) Find the probability that they are both white.
Answer: ............................................... [2]

(b) Find the probability that one is white and one is red.
Answer: ............................................... [3]

Question 4:

Paul buys a number of large sacks of fertiliser costing \( x \) dollars each.
He spends $27.
(a) Write down, in terms of \( x \), an expression for the number of large sacks which Paul buys.
Answer: ............................................... [1]

(b) Rula buys a number of small sacks of fertiliser.
Each small sack costs $2 less than a large sack.
Rula spends $25.
Write down, in terms of \( x \), an expression for the number of small sacks which Rula buys.
Answer: ............................................... [1]

(c) Rula buys 4 more sacks than Paul.
Write down an equation in \( x \) and show that it simplifies to \( 2x^2 - 3x - 27 = 0 \).
Answer: ............................................... [4]

(d) Solve \( 2x^2 - 3x - 27 = 0 \).
Answer: \( x = \) ......................... or \( x = \) ......................... [3]

(e) Calculate the number of sacks which Paul buys.
Answer: ............................................... [1]

Question 5:

The sum of squares follows the pattern:
\[ 1^2 = 1 \]
\[ 1^2 + 2^2 = 5 \]
\[ 1^2 + 2^2 + 3^2 = 14 \]
\[ 1^2 + 2^2 + 3^2 + 4^2 = 30 \]
\[ 1^2 + 2^2 + 3^2 + 4^2 + \dots + n^2 = an^3 + bn^2 + \frac{n}{6} \]
Work out the values of \( a \) and \( b \).
Answer:
\( a = \) ...............................................
\( b = \) ............................................... [6]

Question 6:

The distance a train travels on a journey is 600 km.
(a) Write down an expression, in terms of \( x \), for the average speed of the train when:
(i) the journey takes \( x \) hours,
Answer: ....................................... km/h [1]

(ii) the journey takes \( (x + 1) \) hours.
Answer: ....................................... km/h [1]

(b) The difference between the average speeds in part (a)(i) and part (a)(ii) is 20 km/h.
(i) Show that \( x^2 + x - 30 = 0 \).
Answer: ....................................... [3]

(ii) Find the average speed of the train for the journey in part (a)(ii).
Show all your working.
Answer: ....................................... km/h [4]

Question 7:

(a) Jamil, Kiera and Luther collect badges.
Jamil has \( x \) badges.
Kiera has 12 badges more than Jamil.
Luther has 3 times as many badges as Kiera.
Altogether they have 123 badges.
Form an equation and solve it to find the value of \( x \).
Answer: \( x = \) ......................................... [3]

(b) Find the integer values of \( t \) which satisfy the inequalities:
\( 4t + 7 < 39 \leq 7t + 2 \)
Answer: ......................................... [3]

(c) Solve the following equations:
(i) \((21 - x)(x + 3) = 4 \)
Answer: \( x = \) ......................................... [3]

(ii) \( 3x^2 + 7x - 5 = 0 \)
Show all your working and give your answers correct to 2 decimal places.
Answer: \( x = \) .................. or \( x = \) .................. [4]

Question 8:

On the first part of a journey, Alan drove a distance of \( x \) km and his car used 6 litres of fuel.
The rate of fuel used by his car was \( \frac{600}{x} \) litres per 100 km.

(a) Alan then drove another \( (x + 20) \) km and his car used another 6 litres of fuel.
(i) Write down an expression, in terms of \( x \), for the rate of fuel used by his car on this part
of the journey. Give your answer in litres per 100 km.
Answer: ......................................... litres per 100 km [1]

(ii) On this part of the journey the rate of fuel used by the car decreased by 1.5 litres per 100 km.
Show that \( x^2 + 20x - 8000 = 0 \).
Answer: ......................................... [4]

(b) Solve the equation \( x^2 + 20x - 8000 = 0 \).
Answer: \( x = \) ............................... or \( x = \) ............................... [3]

(c) Find the rate of fuel used by Alan’s car for the complete journey.
Give your answer in litres per 100 km.
Answer: ......................................... litres per 100 km [2]

Question 9:

(d) \( n \) is an integer.
(i) Explain why \( 2n - 1 \) is an odd number.
Answer: ................................................................................................................................
..................................................................................................................................................... [1]

(ii) Write down, in terms of \( n \), the next odd number after \( 2n - 1 \).
Answer: ................................................ [1]

(iii) Show that the difference between the squares of two consecutive odd numbers is a multiple of 8.
Answer: ................................................................................................................................ [3]

Question 10:

(a) The total surface area of a cone is given by the formula: \[ A = \pi r l + \pi r^2 \]
(i) Find \( A \) when \( r = 6.2 \) cm and \( l = 10.8 \) cm.
Answer: .......................................... cm² [2]

(ii) Rearrange the formula to make \( l \) the subject.
Answer: \( l = \) ................................................. [2]

(b) (i) Irina walks 10 km at 4 km/h and then a further 8 km at 5 km/h.
Calculate Irina’s average speed for the whole journey.
Answer: ........................................ km/h [3]

(ii) Dariella walks \( x \) km at 5 km/h and then runs \( (x + 4) \) km at 10 km/h.
The average speed of this journey is 7 km/h.
Find the value of \( x \). Show all your working.
Answer: \( x = \) ................................................. [5]

Question 11:

(a) The perimeter of the rectangle is 80 cm.
The area of the rectangle is \( A \) cm².
(i) Show that: \[ x^2 - 40x + A = 0 \]
[3]

(ii) When \( A = 300 \), solve by factorizing the equation: \[ x^2 - 40x + 300 = 0 \]
Answer: \( x = \) ..................... or \( x = \) .................... [3]

(iii) When \( A = 200 \), solve using the quadratic formula: \[ x^2 - 40x + 200 = 0 \]
Show all your working and give your answers correct to 2 decimal places.
Answer: \( x = \) ..................... or \( x = \) .................... [4]

(b) A car completes a 200 km journey with an average speed of \( x \) km/h.
The return journey is 200 km with an average speed of \( (x + 10) \) km/h.
(i) Show that the difference between the time taken for both journeys is: \[ \frac{2000}{x(x + 10)} \]
[3]

(ii) Find the difference in time taken for both journeys when \( x = 80 \).
Give your answer in minutes and seconds.
Answer: .................... min .................... s [3]

Question 12:

(a) Work out the value of \( x \) in each of the following:
(i) \( 3^x = 243 \)
Answer: \( x = \) ..................... [1]

(ii) \( 16^x = 4 \)
Answer: \( x = \) ..................... [1]

(iii) \( 8^x = 32 \)
Answer: \( x = \) ..................... [2]

(iv) \( 27^x = \frac{1}{9} \)
Answer: \( x = \) ..................... [2]

(b) Solve by factorization:
\( y^2 - 7y - 30 = 0 \)
Show your working.
Answer: \( y = \) ................... or \( y = \) ................... [3]

Question 13:

Alfonso runs 10 km at an average speed of \( x \) km/h.
The next day he runs 12 km at an average speed of \( (x - 1) \) km/h.
The time taken for the 10 km run is 30 minutes less than the time taken for the 12 km run.

(a) (i) Write down an equation in \( x \) and show that it simplifies to \( x^2 - 5x - 20 = 0 \).
Answer: ............................................. [4]

(ii) Use the quadratic formula to solve the equation \( x^2 - 5x - 20 = 0 \).
Show your working and give your answers correct to 2 decimal places.
Answer: \( x = \) ....................... or \( x = \) ....................... [4]

(iii) Find the time that Alfonso takes to complete the 12 km run.
Give your answer in hours and minutes correct to the nearest minute.
Answer: ................ hours ................ minutes [2]

Question 14:

Town A has a rectangular park.
The length of the park is \( x \) m.
The width of the park is 25 m shorter than the length.
The area of the park is 2200 m².

(i) Show that \( x^2 - 25x - 2200 = 0 \).
Answer: ............................................. [1]

(ii) Solve \( x^2 - 25x - 2200 = 0 \).
Show all your working and give your answers correct to 2 decimal places.
Answer: \( x = \) ..................... or \( x = \) ..................... [4]

Question 15:

(a) Simplify:
(i) \( (3p^2)^5 \)
Answer: ............................................. [2]
(ii) \( \frac{18x^2y^6}{2xy^2} \)
Answer: ............................................. [2]
(iii) \[ \left(\frac{4}{m}\right)^{-2} \]
Answer: ............................................. [1]

(b) In this part, all measurements are in metres.
The diagram shows a rectangle with dimensions:
Length = \( 5x - 9 \), Width = \( 3x + 7 \).
The area of the rectangle is 310 m².
Work out the value of \( w \).
Answer: \( w = \) ............................................. [4]

Question 16:

(a) At a football match, the price of an adult ticket is $x, and the price of a child ticket is \( x - 2.50 \).
There are 18,500 adults and 2,400 children attending.
The total amount paid is $320,040.
Find the price of an adult ticket.
Answer: $ ............................................. [4]

(b) (i) Factorise \( y^2 + 5y - 84 \).
Answer: ............................................. [2]
(ii) The area of the rectangle is 84 cm².
Length = \( y + 5 \), Width = \( y \).
Find the perimeter.
Answer: .......................................... cm [3]

(c) In a shop:
- The price of a monthly magazine is $m.
- The price of a weekly magazine is \( m - 0.75 \).
The shop receives:
- $168 from monthly magazines.
- $207 from weekly magazines.
The total number of magazines sold is 100.
(i) Show that \( 50m^2 - 225m + 63 = 0 \).
[3]
(ii) Find the price of a monthly magazine.
Answer: $ ............................................. [3]