MATHS

Question 1:

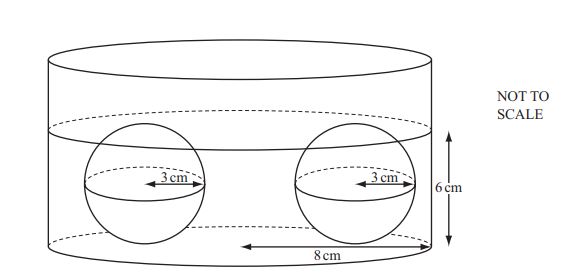
The diagram shows two solid spheres of radius 3 cm lying on the base of a cylinder of radius 8 cm.
Liquid is poured into the cylinder until the spheres are just covered.
[The volume, \( V \), of a sphere with radius \( r \) is \( V = \frac{4}{3} \pi r^3 \).]

(a) Calculate the volume of liquid in the cylinder in:
(i) cm³
Answer: ............................... cm³ [4]
(ii) litres
Answer: ............................... litres [1]

(b) One cubic centimetre of the liquid has a mass of 1.22 grams.
Calculate the mass of the liquid in the cylinder in kilograms.
Answer: ............................... kg [2]

(c) The spheres are removed from the cylinder.
Calculate the new height of the liquid in the cylinder.
Answer: ............................... cm [2]

Question 2:

(a) The running costs for a papermill are $75,246.
This amount is divided in the ratio labour costs:materials = 5:1.
Calculate the labour costs.
Answer: $ ........................................... [2]

(b) In 2012 the company made a profit of $135,890.
In 2013 the profit was $150,675.
Calculate the percentage increase in the profit from 2012 to 2013.
Answer: ........................................... % [3]

(c) The profit of $135,890 in 2012 was an increase of 7% on the profit in 2011.
Calculate the profit in 2011.
Answer: $ ........................................... [3]

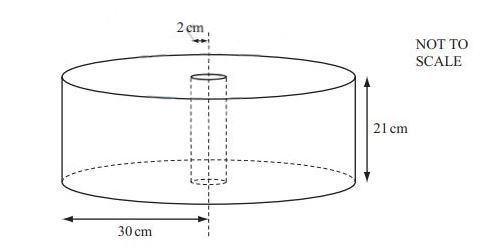
(d) Paper is sold in cylindrical rolls.
There is a wooden cylinder of radius 2cm and height 21cm in the centre of each roll.
The outer radius of a roll of paper is 30cm.
(i) Calculate the volume of paper in a roll.
Answer: ......................................... cm³ [3]

(ii) The paper is cut into sheets which measure 21cm by 29.7cm.
The thickness of each sheet is 0.125mm.
(a) Change 0.125 millimetres into centimetres.
Answer: ......................................... cm [1]
(b) Work out how many whole sheets of paper can be cut from a roll.
Answer: ......................................... [4]

Question 3:

The total surface area of a cone with radius x and slant height 3x is equal to the area of a circle with radius r.
Show that r = 2x.
[The curved surface area, A, of a cone with radius r and slant height l is A = πrl.]
Answer: ......................................... [4]

Question 4:

(a) Calculate the volume of a metal sphere of radius 15 cm and show that it rounds to 14,140 cm³, correct to 4 significant figures.
[The volume, V, of a sphere with radius r is \( V = \frac{4}{3} \pi r^3 \)]

(b) (i) The sphere is placed inside an empty cylindrical tank of radius 25 cm and height 60 cm. The tank is filled with water.


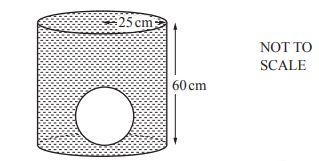
Calculate the volume of water required to fill the tank.

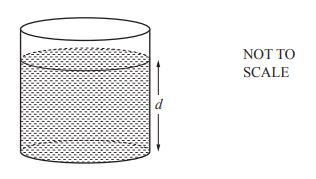
(ii) The sphere is removed from the tank. Calculate the depth, d, of water in the tank.

(c) The sphere is melted down and the metal is made into a solid cone of height 54 cm.
(i) Calculate the radius of the cone.
[The volume, V, of a cone with radius r and height h is \( V = \frac{1}{3} \pi r^2 h \)]

(ii) Calculate the total surface area of the cone.
[The curved surface area, A, of a cone with radius r and slant height l is \( A = \pi r l \)]

Question 5:

(a) The diagram shows a solid metal prism with cross section ABCDE.


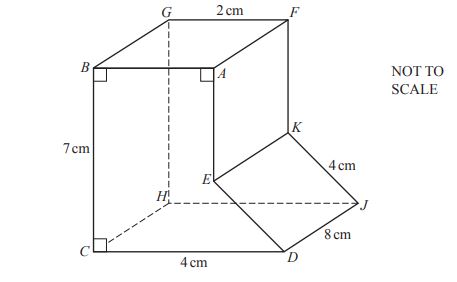
(i) Calculate the area of the cross section ABCDE.

(ii) The prism is of length 8 cm. Calculate the volume of the prism.

(b) A cylinder of length 13 cm has volume 280 cm³.
(i) Calculate the radius of the cylinder.

(ii) The cylinder is placed in a box that is a cube of side 14 cm.
Calculate the percentage of the volume of the box that is occupied by the cylinder.

Question 6:

(a) A solid hemisphere has volume 230 cm³.
Calculate the radius of the hemisphere.
[The volume, V, of a sphere with radius r is V = (4/3)πr³]

(b) A solid cylinder with radius 1.6 cm is attached to the hemisphere to make a toy.
The total volume of the toy is 300 cm³.


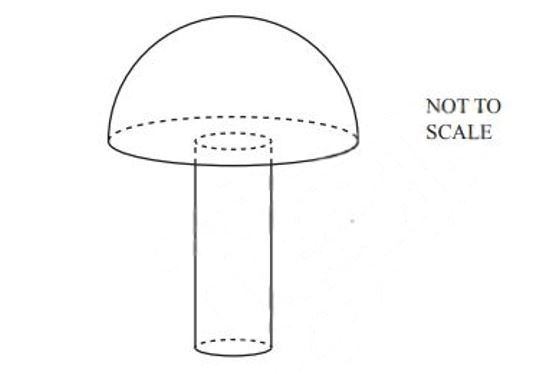
(i) Calculate the height of the cylinder.

(ii) A mathematically similar toy has a volume of 19,200 cm³.
Calculate the radius of the cylinder for this toy.

Question 7:

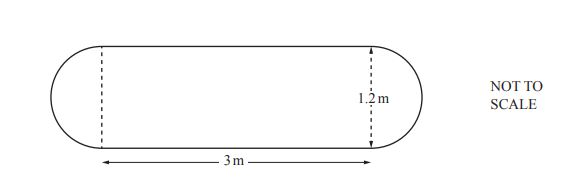
(a) The diagram shows the surface of a garden pond, made from a rectangle and two semicircles.
The rectangle measures 3 m by 1.2 m.
Calculate the area of this surface.

(b) The pond is a prism, and the water in the pond has a depth of 20 cm.
Calculate the number of litres of water in the pond.

(c) After rainfall, the number of litres of water in the pond is 1007.
Calculate the increase in the depth of water in the pond.
Give your answer in centimetres.

Question 8:

(a) A cube with side length \( x \) cm has a volume of 1000 cm³.
Calculate the value of \( x \).

(b) A sphere with radius \( x \) cm has a volume of 1000 cm³.
\[ V = \frac{4}{3} \pi r^3 \]
Calculate the value of \( x \).

(c) A cone with radius \( x \) cm and slant height \( x+5 \) cm has a volume of 1000 cm³.
\[ V = \frac{1}{3} \pi r^2 h \]
Calculate the value of \( x \).

(d) A prism with a right-angled triangle as its cross-section has a volume of 1000 cm³.
Calculate the value of \( x \).

Question 9:

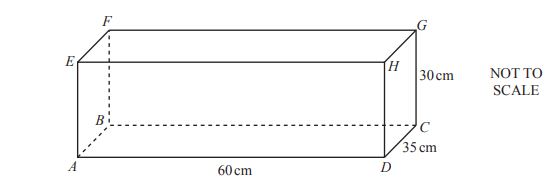
The diagram shows a cuboid.
Given:
- \( AD = 60 \, \text{cm} \)
- \( CD = 35 \, \text{cm} \)
- \( CG = 30 \, \text{cm} \)

(a) Write down the number of planes of symmetry of this cuboid.
Answer: .................................................. [1]

(b)(i) Work out the surface area of the cuboid.
Answer: ........................................... cm² [3]
(ii) Write your answer to part (b)(i) in square metres.
Answer: ............................................. m² [1]

(c)(i) Calculate the length \( AG \).
AG = ............................................ cm [4]
(ii) The angle between \( AG \) and the base \( ABCD \).
Answer: .................................................. [3]

(d)(i) Show that the volume of the cuboid is 63 000 cm³.
[1]
(ii) A cylinder of height 40 cm has the same volume as the cuboid.
Calculate the radius of the cylinder.
Answer: ............................................. cm [3]

Question 10:

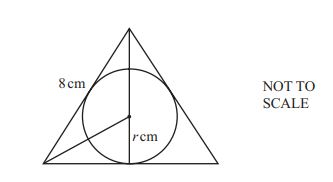
(a) The three sides of an equilateral triangle are tangents to a circle of radius r cm.
The sides of the triangle are 8 cm long.
Calculate the value of r.
Show that it rounds to 2.3, correct to 1 decimal place.

Answer (a): ................................................. cm [3]

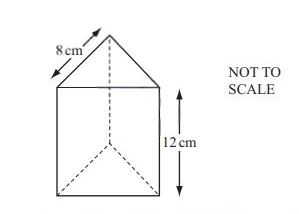
(b) The diagram shows a box in the shape of a triangular prism of height 12 cm.
The cross section is an equilateral triangle of side 8 cm.
Calculate the volume of the box.

Answer (b): ................................................. cm³ [4]

(c) The box contains biscuits. Each biscuit is a cylinder of radius 2.3 cm and height 4 mm.
(i) Calculate the largest number of biscuits that can be placed in the box.
Answer (c)(i): ................................................. [3]
(ii) Calculate the volume of one biscuit in cubic centimetres.
Answer (c)(ii): ................................................. cm³ [2]
(iii) Calculate the percentage of the volume of the box not filled with biscuits.
Answer (c)(iii): ................................................. % [3]

Question 11:

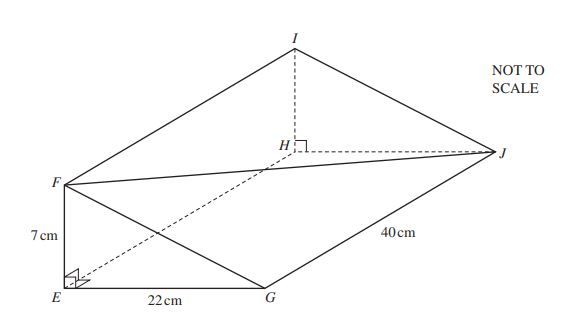
EFGHIJ is a solid metal prism of length 40 cm.
The cross section EFG is a right-angled triangle.
EF = 7 cm and EG = 22 cm.

(a) Calculate the volume of the prism.
Answer (a): ......................................... cm³ [2]

(b) Calculate the length FJ.
Answer (b) FJ = ......................................... cm [4]

(c) Calculate the angle between FJ and the base EGJH of the prism.
Answer (c): ......................................... [3]

(d) The prism is melted and made into spheres. Each sphere has a radius of 1.5 cm.
Work out the greatest number of spheres that can be made.
[The volume, \( V \), of a sphere with radius \( r \) is \( V = \frac{4}{3} \pi r^3 \).]
Answer (d): ......................................... [3]

(e)
(i) A right-angled triangle is the cross section of another prism.
This triangle has height 4.5 cm and base 11.0 cm.
Both measurements are correct to 1 decimal place.
Calculate the upper bound for the area of this triangle.
Answer (e)(i): ......................................... cm² [2]
(ii) Write your answer to part (e)(i) correct to 4 significant figures.
Answer (e)(ii): ......................................... cm² [1]