MATHS

Question 1:

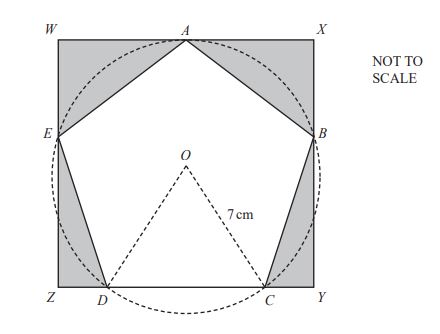
The vertices \( A, B, C, D, \) and \( E \) of a regular pentagon lie on the circumference of a circle, center \( O \), radius 7 cm. They also lie on the sides of a rectangle \( WXYZ \).

(a) Show that:
(i) \( \angle DOC = 72^\circ \)
Answer: ................................................. [1]

(ii) \( \angle DCB = 108^\circ \)
Answer: ................................................. [2]

(iii) \( \angle CBY = 18^\circ \)
Answer: ................................................. [1]

(b) Show that the length \( CD \) of one side of the pentagon is **8.23 cm** correct to three significant figures.
Answer: ................................................. [3]

(c) Calculate:
(i) The area of the triangle \( DOC \)
Answer: ........................ cm² [2]

(ii) The area of the pentagon \( ABCDE \)
Answer: ........................ cm² [1]

(iii) The area of the sector \( ODC \)
Answer: ........................ cm² [2]

(iv) The length \( XY \)
Answer: ........................ cm [2]

(d) Calculate the ratio:
**Area of pentagon \( ABCDE \) : Area of rectangle \( WXYZ \)** Give your answer in the form **1 : n**.
Answer: **1 :** ...................... [5]

Question 2:

(a) The diagram shows a circle with two chords, \( AB \) and \( CD \), intersecting at \( X \).

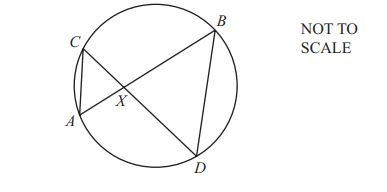
(i) Show that triangles \( ACX \) and \( DBX \) are similar.
Answer: ................................................. [2]

(ii) Given:

• \( AX = 3.2 \) cm
• \( BX = 12.5 \) cm
• \( CX = 4 \) cm
• \( \angle AXC = 110^\circ \)

(a) Find \( DX \).
Answer: \( DX = \) .......................................... cm [2]

(b) Use the **cosine rule** to find \( AC \).
Answer: \( AC = \) .......................................... cm [4]

(c) Find the **area of triangle** \( BXD \).
Answer: ......................................... cm² [2]

(b) Height of a flagpole on top of a building:
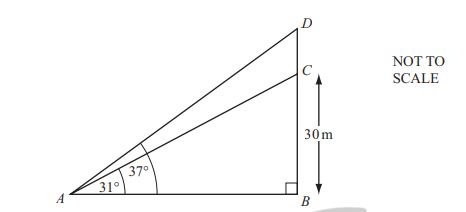
In the diagram:

• **BC** represents a **building** of height **30m**.
• A **flagpole**, \( DC \), stands on top of the building.
• From a point \( A \), the **angle of elevation** of the **top of the building** is **31°**.
• The **angle of elevation** of the **top of the flagpole** is **37°**.

Calculate the **height \( DC \)** of the flagpole.
Answer: ............................................ m [5]

Question 3:

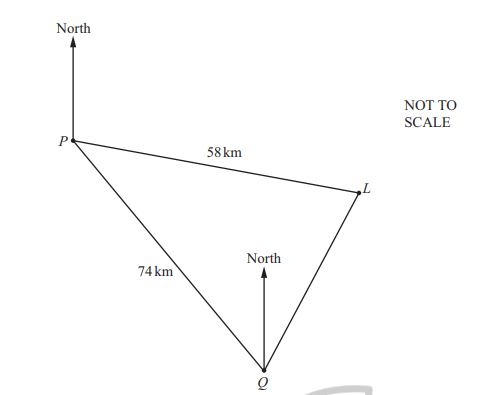
A ship sails from port \( P \) to port \( Q \).
\( Q \) is **74 km** from \( P \) on a **bearing of 142°**.
A **lighthouse**, \( L \), is **58 km** from \( P \) on a **bearing of 110°**.

(a) Show that the **distance \( LQ \)** is **39.5 km** correct to **1 decimal place**.
Answer: ................................................. [5]

(b) Use the **sine rule** to calculate **angle \( PQL \)**.
Answer: \( \angle PQL = \) ................................................ [3]

(c) Find the **bearing of**:
(i) \( P \) **from** \( Q \)
Answer: ................................................ [2]

(ii) \( L \) **from** \( Q \)
Answer: ................................................ [1]

(d) The ship takes **2 hours and 15 minutes** to sail the **74 km** from \( P \) to \( Q \).
Calculate the **average speed** in **knots**.
[1 knot = 1.85 km/h]
Answer: ....................................... knots [3]

(e) Calculate the **shortest distance** from the **lighthouse** to the **path of the ship**.
Answer: .......................................... km [3]

Question 4:

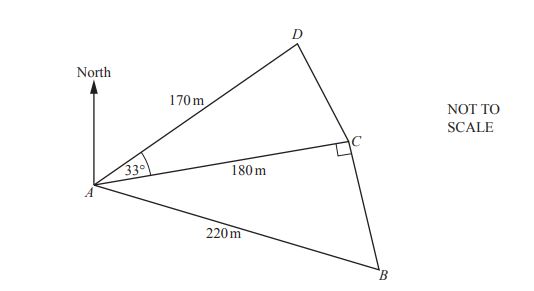
The diagram shows **five straight footpaths** in a park.
\( AB = 220 \) m, \( AC = 180 \) m, and \( AD = 170 \) m.
\(\angle ACB = 90^\circ\) and \(\angle DAC = 33^\circ\).

(a) Calculate **BC**.
Answer: \( BC = \) ............................................ m [3]

(b) Calculate **CD**.
Answer: \( CD = \) ............................................ m [4]

(c) Calculate the **shortest distance** from \( D \) to \( AC \).
Answer: ............................................ m [2]

(d) The **bearing of \( D \) from \( A \) is 047°**.
Calculate the **bearing of \( B \) from \( A \)**.
Answer: ................................................ [3]

(e) Calculate the **area of the quadrilateral \( ABCD \)**.
Answer: ............................................ \( m^2 \) [3]

Question 5:

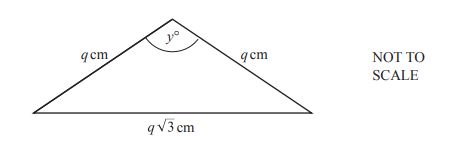
The perimeter of the **isosceles triangle** is \[ 2q + q\sqrt{3} \] centimetres.
Find the value of \( y \).
Answer: \( y = \) ................................................ [4]

Question 6:

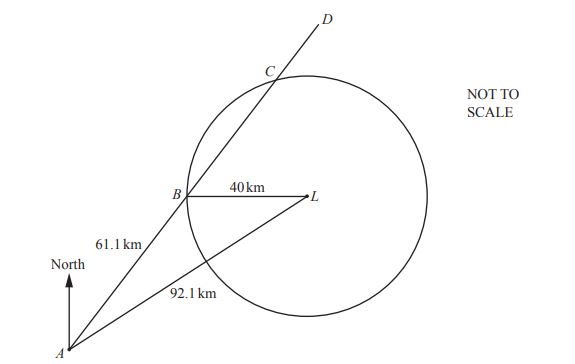
The diagram shows the position of a port \( A \) and a lighthouse \( L \).
The circle, center \( L \) and radius **40 km**, shows the region where the light from the lighthouse can be seen.
The straight line, **ABCD**, represents the course taken by a ship after leaving the port.
When the ship reaches position \( B \), it is **due west** of the lighthouse.
Given: \( AL = 92.1 \) km, \( AB = 61.1 \) km, \( BL = 40 \) km.

(a) Use the **cosine rule** to show that **angle ABL = 130.1°**, correct to 1 decimal place.
Answer: ................................................... [4]

(b) Calculate the **bearing** of the lighthouse, \( L \), from the port, \( A \).
Answer: ................................................... [4]

(c) The ship sails at a speed of **28 km/h**.
Calculate the length of time for which the light from the lighthouse can be seen from the ship.
Give your answer **correct to the nearest minute**.
Answer: .................... h .................... min [5]

Question 7:

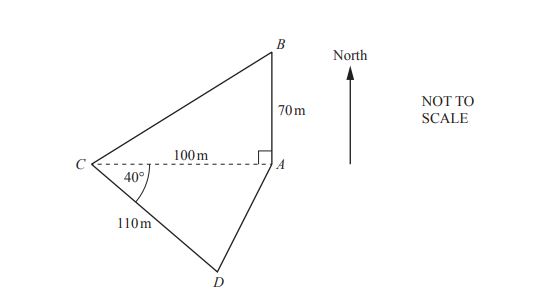
The diagram shows a field **ABCD**.

(a) Calculate the **area** of the field ABCD.
Answer: ............................................m² [3]

(b) Calculate the **perimeter** of the field ABCD.
Answer: ............................................m [5]

(c) Calculate the **shortest distance from A to CD**.
Answer: ............................................m [2]

(d) \( B \) is due **north** of \( A \).
Find the **bearing of C from B**.
Answer: ................................................. [3]

Question 8:

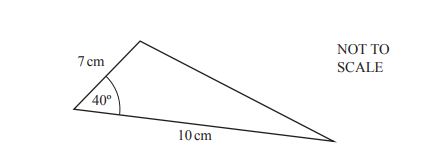
**(a)** A triangle has sides **7 cm** and **10 cm**, with an **included angle of 40°**.
(i) Calculate the **area** of the triangle.
Answer: ............................................cm² [2]

(ii) Calculate the **perimeter** of the triangle and show that it is **23.5 cm**, correct to **1 decimal place**.
Show all your working.
Answer: ............................................cm [5]

**(b)** A sector of a circle has a **radius of 9 cm**, and its **perimeter is 28.2 cm**.
Calculate the value of **c**.
Answer: **c =** ............................................° [3]

Question 9:

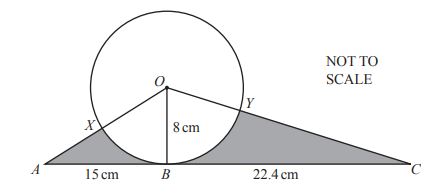
A **circle** has **center O**. The **tangent ABC** touches the circle at **B**.
Given: **OB = 8 cm**, **AB = 15 cm**, **BC = 22.4 cm**.
The line **AO** crosses the circle at **X**, and **OC** crosses the circle at **Y**.

(a) Calculate **angle XOY**.
Answer: **Angle XOY =** ............................................° [5]

(b) Calculate the **length of the arc XBY**.
Answer: ............................................ cm [2]

(c) Calculate the **total area of the two shaded regions**.
Answer: ............................................ cm² [4]

Question 10:

The diagram shows the positions of three cities: **Geneva (G), Budapest (B), and Hamburg (H)**.

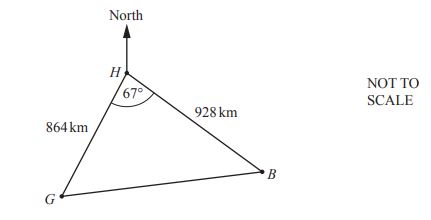
(a) A plane flies from Geneva to Hamburg.
The flight takes **2 hours 20 minutes**.
Calculate the **average speed** in km/h.
Answer: **............................... km/h** [2]

(b) Use the **cosine rule** to calculate the distance from **Geneva to Budapest**.
Answer: **............................... km** [4]

(c) The bearing of **Budapest from Hamburg** is **133°**.

(i) Find the bearing of **Hamburg from Budapest**.
Answer: **...............................** [2]

(ii) Calculate the **bearing of Budapest from Geneva**.
Answer: **...............................** [4]