MATHS

Question 1:

(a) Solve the equations:
(i) \[ 4x - 7 = 8 - 2x \]
Answer: \( x = \) ................................................. [2]

(ii) \[ \frac{x - 7}{3} = 2 \]
Answer: \( x = \) ................................................. [2]

(b) Simplify the expressions:
(i) \[ (3xy^4)^3 \]
Answer: ................................................. [2]

(ii) \[ (16a^6b^2)^{\frac{1}{2}} \]
Answer: ................................................. [2]

(iii) \[ \frac{x^2-7x-8}{x^2-64} \]
Answer: ................................................. [4]

Question 2:

(a) (i) Factorise completely the expression:
\[ 4x^2 - 18x - 10 \]
Answer: ................................................. [3]

(ii) Solve:
\[ 4x^2 - 18x - 10 = 0 \]
Answer: \( x = \) .......... or \( x = \) .......... [1]

(b) Solve the equation:
\[ 2x^2 - 7x - 10 = 0 \]
Show all your working and give your answers correct to two decimal places.
Answer: \( x = \) .......... or \( x = \) .......... [4]

(c) Write the following as a single fraction in its simplest form:
\[ \frac{6}{3x - 1} - \frac{2}{x- 2} \]
Answer: ................................................. [3]

Question 3:

(a) Write as a single fraction in its simplest form:
\[ \frac{2x-1}{2} - \frac{3x + 1}{5} \]
Answer: ................................................. [3]

(b) Expand and simplify:
\[ (2x - 3)^2 - 3x(x - 4) \]
Answer: ................................................. [4]

(c) (i) Factorise:
\[ 2x^2 + 5x - 3 \]
Answer: ................................................. [2]

(ii) Simplify:
\[ \frac{2x^2 +5x -3}{2x^2 - 18} \]
Answer: ................................................. [3]

(d) The trapezium ABCD has four angles as shown (all in degrees):
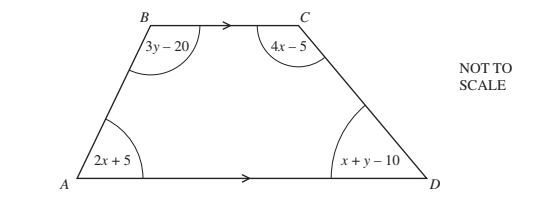
\( 3y - 20 \), \( 4x - 5 \), \( 2x + 5 \), \( x + y - 10 \)

(i) Show that:
\[ 7x + 4y = 390 \]
Answer: ................................................. [1]

(ii) Show that:
\[ 2x + 3y = 195 \]
Answer: ................................................. [1]

(iii) Solve these simultaneous equations:
Answer: \( x = \) .......... , \( y = \) .......... [4]

(iv) Use your answer from part (d)(iii) to find the sizes of all four angles of the trapezium:
Answer: .......... , .......... , .......... , .......... [1]

Question 4:

(a) Rearrange the equation to make \( a \) the subject:
\[ s = ut + \frac{1}{2}at^2 \]
Answer: \( a = \) ................................................. [3]

(b) The formula \( v = u + at \) can be used to calculate the speed \( v \) of a car. Given: \[ u = 15, \quad a = 2, \quad t = 8 \] (each correct to the nearest integer). Calculate the **upper bound** of the speed \( v \).
Answer: ................................................. [3]

Question 5:

(a) Simplify:
\[ \frac{x^2 - 3x}{ x^2 - 9} \]
Answer: ................................................. [3]

(b) Solve:
\[ \frac{15}{x} - \frac{20}{x+1} = 2 \]
Answer: \( x = \) ............... or \( x = \) ............... [7]

Question 6:

(a) Expand and simplify:
(i) \[ 4(2x - 1) - 3(3x - 5) \]
Answer: ................................................. [2]

(ii) \[ (2x - 3y)(3x + 4y) \]
Answer: ................................................. [3]

(b) Factorise:
\[ x^3 - 5x \]
Answer: ................................................. [1]

(c) Solve the inequality:
\[ \frac{2x+3}{3} \geq \frac{5x-8}{4} \]
Answer: ................................................. [3]

(d) Given:
\[ x^2 - 9x + 12 = (x - p)^2 - q \]
(i) Find the values of \( p \) and \( q \).
Answer: \( p = \) ................................................
Answer: \( q = \) ................................................ [3]

(ii) Write down the minimum value of \( x^2 - 9x + 12 \).
Answer: ................................................. [1]

(iii) Write down the equation of the line of symmetry of the graph of \( y = x^2 - 9x + 12 \).
Answer: ................................................. [1]

Question 7:

(a) Solve the inequality:
\[ 7x - 5 > 3(2 - 5x) \]
Answer: ................................................. [3]

(b) (i) Factorise completely:
\[ pq - 2q - 8 + 4p \]
Answer: ................................................. [2]

(ii) Factorise:
\[ 9p^2 - 25 \]
Answer: ................................................. [1]

(c) Solve this equation by factorising:
\[ 5x^2 + x - 18 = 0 \]
Answer: \( x = \) ....................... or \( x = \) ....................... [3]

Question 8:

(a) Simplify:
(i) \[ \frac{x^3}{\frac{3}{x^5}} \]
Answer: ................................................. [1]

(ii) \[ 5xy^8 \times 3x^6y^{-5} \]
Answer: ................................................. [2]

(iii) \[ \left( 64x^{12} \right)^{\frac{2}{3}} \]
Answer: ................................................. [2]

(b) Solve the equation:
\[ 3x^2 - 7x - 12 = 0 \]
Show all your working and give your answers correct to 2 decimal places.
Answer: \( x = \) ........................ or \( x = \) ........................ [4]

(c) Simplify:
\[ \frac{x^2 - 25}{x^3-5x^2} \]
Answer: ................................................. [3]

Question 9:

(a) A quadrilateral has side lengths:
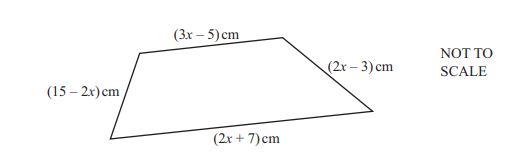
\[ (3x - 5) \text{ cm}, \quad (2x - 3) \text{ cm}, \quad (2x + 7) \text{ cm}, \quad (15 - 2x) \text{ cm} \]
(i) Write an expression, in terms of \( x \), for the perimeter of the quadrilateral.
Answer: .......................................... cm [2]

(ii) The perimeter of the quadrilateral is 32 cm.
Find the length of the longest side of the quadrilateral.
Answer: .......................................... cm [3]

(b) A triangle and a quadrilateral have the following side lengths:
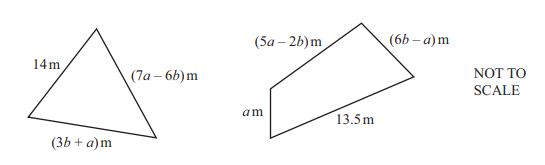
Triangle:
\[ 14m, \quad (3b + a)m, \quad (7a - 6b)m \]
Quadrilateral:
\[ (5a - 2b)m, \quad (6b - a)m, \quad 13.5m, \quad am \]
The triangle has a perimeter of 32.5 m.
The quadrilateral has a perimeter of 39.75 m.
Write two equations in terms of \( a \) and \( b \) and simplify them.
Use an algebraic method to find the values of \( a \) and \( b \).
Show all your working.
Answer: \( a = \) ................................................
\( b = \) ................................................ [6]

Question 10:

(a) Factorise \( x^2 - 3x - 10 \).
Answer: ................................................ [2]

(b) (i) Show that
\[ \frac{x + 2}{x + 1} + \frac{3}{x} = 3 \]
simplifies to
\[ 2x^2 - 2x - 3 = 0. \]
Answer: ................................................ [3]

(ii) Solve \( 2x^2 - 2x - 3 = 0 \).
Give your answers correct to 3 decimal places.
Show all your working.
Answer: \( x = \) ........................... or \( x = \) ........................... [4]

(c) Simplify
\[ \frac{2x + 3}{x + 2} - \frac{x}{x+1} \]
Answer: ................................................ [4]

Question 11:

(a) Solve:
\[ 8x - 5 = 22 - 4x \]
Answer: \( x = \) .................................................. [2]

(b) Solve:
\[ 6x >= 2x + 14 \]
Answer: ................................................... [2]

(c) Factorise:
\[ x^2 - 4x - 21 \]
Answer: ................................................... [2]

(d) Expand the brackets and simplify:
\[ (3x - 2y)(4x + 3y) \]
Answer: ................................................... [3]

Question 12:
Solve:
\[ \frac{2}{x+3} + \frac{1}{12} = \frac{3}{2x - 1} \]
Answer: \( x = \) ..................... or \( x = \) ..................... [7]

Question 13:
(a) Solve:
\[ 11x + 15 = 3x - 7 \]
Answer: \( x = \) ..................... [2]

(b) (i) Factorise:
\[ x^2 + 9x - 22 \]
Answer: ................................................ [2]

(ii) Solve:
\[ x^2 + 9x - 22 = 0 \]
Answer: \( x = \) ..................... or \( x = \) ..................... [1]

(c) Rearrange:

\[ y = \frac{2(x - a)}{x} \]

to make \( x \) the subject.
Answer: \( x = \) ................................................ [4]

(d) Simplify:
\[ \frac{x^2 - 6x}{x^2 - 36} \]
Answer: ................................................ [3]

Question 14:

(a) Solve:
\[ \frac{x}{7} = 49 \]
Answer: \( x = \) ................................................. [1]

(b) Simplify:
(i) \[ x^0 \]
Answer: ................................................. [1]

(ii) \[ x^7 \times x^3 \]
Answer: ................................................. [1]

(iii) \[ \frac{(3x^6)^2}{x^{-4}} \]
Answer: ................................................. [2]

(c) (i) Factorise completely:
\[ 2x^2 - 8 \]
Answer: ................................................. [2]

(ii) Simplify:
\[ \frac{2x^2 -18}{x^2 + 7x - 30} \]
Answer: ................................................. [3]

Question 15:

(a) Factorise:
\[ 5m^2 - 20p^4 \]
Answer: ................................................. [3]

(b) Make \( P \) the subject of the formula:
\[ A = P + \frac{PRT}{100} \]
Answer: \( P = \) ................................................. [3]

Question 16:

(a) Solve:
\[ 30 + 2x = 3(3 - 4x) \]
Answer: \( x = \) ................................................. [3]

(b) Factorise:
\[ 12ab^3 + 18a^3b^2 \]
Answer: ................................................. [2]

(c) Simplify:
(i) \[ 5a^3c^2 \times 2a^2c^7 \]
Answer: ................................................. [2]

(ii) \[ \left( \frac{16a^8}{c^{12}} \right)^{\frac{3}{4}} \]
Answer: ................................................. [2]

(d) \( y \) is inversely proportional to the square of \( (x + 2) \). When \( x = 3 \), \( y = 2 \). Find \( y \) when \( x = 8 \).
Answer: \( y = \) ................................................. [3]

(e) Write as a single fraction in its simplest form:
\[ \frac{5}{x-2} - \frac{x-5}{2} \]
Answer: ................................................. [3]